若f(x)的导函数f′(x)=—2x^2+1,且f(1)=1,求f(x)
 SSDD1292022-10-04 11:39:541条回答
SSDD1292022-10-04 11:39:541条回答
已提交,审核后显示!提交回复
共1条回复
 tianshaguxing 共回答了14个问题
tianshaguxing 共回答了14个问题 |采纳率92.9%- f'(x)=-2x²+1
则f(x)=-x³+x+C
f(1)=-1+1+C=1
所以C=1
所以f(x)=-x³+x+1 - 1年前
相关推荐
- (2013•郑州二模)函数f(x)的定义域为开区间(a,b),导函数f′(x)在(a,b)内的图象如图所示,则函数f(x
 (2013•郑州二模)函数f(x)的定义域为开区间(a,b),导函数f′(x)在(a,b)内的图象如图所示,则函数f(x)在开区间(a,b)内有极大值点( )
(2013•郑州二模)函数f(x)的定义域为开区间(a,b),导函数f′(x)在(a,b)内的图象如图所示,则函数f(x)在开区间(a,b)内有极大值点( )
A.1个
B.2个
C.3个
D.4个 syp02021年前1
syp02021年前1 -
 lyaxing 共回答了11个问题
lyaxing 共回答了11个问题 |采纳率81.8%解题思路:根据题目给出的导函数的图象,得到导函数在给定定义域内不同区间上的符号,由此判断出原函数在各个区间上的单调性,从而判断出函数取得极大值的情况. 如图,不妨设导函数的零点分别为x1,x2,x3,x4.
如图,不妨设导函数的零点分别为x1,x2,x3,x4.
由导函数的图象可知:
当x∈(a,x1)时,f′(x)>0,f(x)为增函数,
当x∈(x1,x2)时,f′(x)<0,f(x)为减函数,
当x∈(x2,x3)时,f′(x)>0,f(x)为增函数,
当x∈(x3,x4)时,f′(x)>0,f(x)为增函数,
当x∈(x4,b)时,f′(x)<0,f(x)为减函数,
由此可知,函数f(x)在开区间(a,b)内有两个极大值点,
分别是当x=x1时和x=x4时函数取得极大值.
故选B.点评:
本题考点: 利用导数研究函数的极值.
考点点评: 本题考查了利用导函数研究函数的极值,由导函数在给定区间内的符号可以判断原函数的单调性,连续函数在某点处先增后减,该点是极大值点,先减后增,该点是极小值点.此题是中档题.1年前查看全部
- 已知定义在R上的函数f(x),其导函数f′(x)的大致图象如图所示,则下列叙述正确的是( ) A.f(b)>f(c)>
已知定义在R上的函数f(x),其导函数f′(x)的大致图象如图所示,则下列叙述正确的是( ) A.f(b)>f(c)>f(d) B.f(b)>f(a)>f(c) C.f(c)>f(b)>f(a) D.f(c)>f(b)>f(d) 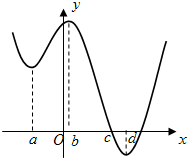
 littlexian1年前1
littlexian1年前1 -
 cxwoool 共回答了16个问题
cxwoool 共回答了16个问题 |采纳率87.5%由导函数f′(x)的大致图象知:当x≤c时,f′(x)≥0,f(x)单调递增,又a<b<c,所以f(c)>f(b)>f(a).
故选C.1年前查看全部
- 下面四个图中有一个是函数f(x)=13x3?ax2+1(a∈R且a≠0)的导函数f′(x)的图象,则f(-1)等于___
下面四个图中有一个是函数f(x)=13x3?ax2+1(a∈R且a≠0)的导函数f′(x)的图象,则f(-1)等于______
下面四个图中有一个是函数f(x)=
x3?ax2+1(a∈R且a≠0)的导函数f′(x)的图象,则f(-1)等于______.1 3 
 ddde专用dd1年前1
ddde专用dd1年前1 -
 156192281 共回答了20个问题
156192281 共回答了20个问题 |采纳率95%∵f(x)=
1
3x3?ax2+1(a∈R且a≠0)
∴f′(x)=x2-2ax,
二次项系数为正得到图象开口向上,没有常数项则导函数的图象过原点
故满足条件的图象是第三个
由导函数的图象可知f′(2)=0,解得a=1
∴f(x)=
1
3x3?x2+1则f(-1)=-[1/3]
故答案为:?
1
31年前查看全部
- 若对可导函数f(x),恒有2f(x)+xf′(x)>0,则f(x)( )
若对可导函数f(x),恒有2f(x)+xf′(x)>0,则f(x)( )
A.恒大于0
B.恒小于0
C.恒等于0
D.和0的大小关系不确定 wangshengdi20051年前1
wangshengdi20051年前1 -
 funk5858 共回答了19个问题
funk5858 共回答了19个问题 |采纳率89.5%解题思路:根据题目给出的条件2f(x)+xf′(x)>0,想到构造函数g(x)=x2f(x),求导后分析该函数的单调性,从而能判出函数的极小值点,进一步得到函数g(x)恒大于0,则有f(x)恒大于0.令g(x)=x2f(x),
则g′(x)=2xf(x)+x2f′(x)
=x(2f(x)+xf′(x)),
因为2f(x)+xf′(x)>0,
所以,当x>0时,g′(x)>0,所以函数g(x)在(0,+∞)上为增函数.
当x<0时,g′(x)<0,所以函数g(x)在(-∞,0)上为减函数.
所以,当x=0时函数g(x)有极小值,也就是最小值为g(0)=0.
所以g(x)=x2f(x)恒大于等于0,
当x≠0时,由x2f(x)恒大于0,可得f(x)恒大于0.
又对可导函数f(x),恒有2f(x)+xf′(x)>0,
取x=0时,有2f(0)+0×f′(0)>0,所以f(0)>0.
综上有f(x)恒大于0.
故选A.点评:
本题考点: 导数的运算.
考点点评: 本题考查了构造函数法,考查利用函数的导函数判断函数的单调性,解答的关键是合理构造出函数,属于基础题.1年前查看全部
- 设函数fx是定义在r上的可导函数 其导函数f′(x) 且有2f(x)+xf′(x)>x^2 则不等式
设函数fx是定义在r上的可导函数 其导函数f′(x) 且有2f(x)+xf′(x)>x^2 则不等式
不等式(x+2014)*2f(x+2014)-4f(-2)>0的解集
(x+2014)^2f(x+2014)-4f(-2)>0 是这个才对 小猪KK1年前1
小猪KK1年前1 -
 黑色概念 共回答了24个问题
黑色概念 共回答了24个问题 |采纳率83.3%取特殊:
设y=ax^2+bx+c,则y'=2ax+b,
代入2f(x)+xf′(x)>x^2得
2(ax^2+bx+c)+x(2ax+b)>x^2,
(4a-1)x^2+3bx+2c>0,
取a=1/4,b=0,c=1,y=f(x)=x^2/4+1,
(x+2014)*2f(x+2014)-4f(-2)>0变为
2(x+2014)[(x+2014)^2/4+1]-4*2>0,①
设u=x+2014,①变为u^3+4u-16>0,
(u-2)(u^2+2u+8)>0,u^2+2u+8>0,
∴u-2>0,
∴x+2012>0,x>-2012,为所求.1年前查看全部
- 已知可导函数f(x)的导函数为g(x),且满足:①[g(x)-1](x-2)>0;②f(2-x)-f(x)=2-2x,记
已知可导函数f(x)的导函数为g(x),且满足:①[g(x)-1](x-2)>0;②f(2-x)-f(x)=2-2x,记a=f(4)-3,b=f(e)-e+1,c=f(-1)+2,则a,b,c的大小顺序为( )
A.a>b>c
B.b>a>c
C.b>c>a
D.a>c>b 秋日私欲1年前1
秋日私欲1年前1 -
 不吃cc 共回答了15个问题
不吃cc 共回答了15个问题 |采纳率86.7%解题思路:比较a,b,c的大小,想到利用函数的单调性,由b=f(e)-e+1和[g(x)-1](x-2)>0想到构造函数h(x)=f(x)-x+1,求导,根据[g(x)-1](x-2)>0可判断函数h(x)的单调性,并对a=f(4)-3、c=f(-1)+2进行等价变形为a=f(4)-4+1、c=f(3)-3+1,根据函数的单调性即可得出a,b,c的大小.∵f(2-x)-f(x)=2-2x是减函数,
根据复合函数的单调性知函数f(x)增函数,
令h(x)=f(x)-x+1
则h′(x)=f′(x)-1=g(x)-1,
∵[g(x)-1](x-2)>0
∴当x>1时,g(x)-1>0,
∴h(x)在(1,+∞)上单调递增;
而a=f(4)-3=a=f(4)-4+1
c=f(-1)+2=f(3)+2-2×3+2=f(3)-2=f(3)-3+1
∴f(4)-4+1>f(3)-3+1>f(e)-e+1;即a>c>b,
故选D.点评:
本题考点: 函数单调性的性质.
考点点评: 此题是个难题.考查利用导数研究函数的单调性,体现了函数的思想,综合性强.同时也考查了学生观察、推理以及创造性地分析问题、解决问题的能力.1年前查看全部
- 1.定义在R上的函数f(x)及其导函数f′(x)的图像都是连续不断的曲线,且对于实数a,b(a0,f′(b)f(b);
1.定义在R上的函数f(x)及其导函数f′(x)的图像都是连续不断的曲线,且对于实数a,b(a0,f′(b)f(b);
(3)存在x.属于[a,b],f(x.) f(a); (4)存在x.属于[a,b],f(a)-f(b)>f′(x.)(a-b)
其中结论正确的个数是( ) A.1 B.2 C.3 D.4
1.定义在R上的函数f(x)及其导函数f′(x)的图像都是连续不断的曲线,且对于实数a,b(a0,f′(b)f(b);
(3)存在x。属于[a,b],f(x。) >=f(a); (4)存在x。属于[a,b],f(a)-f(b)>f′(x。)(a-b)
其中结论正确的个数是( ) A.1 B.2 C.3 D.4 lengao1年前4
lengao1年前4 -
 广鹿岛 共回答了24个问题
广鹿岛 共回答了24个问题 |采纳率87.5%定义在R上的函数f(x)及其导函数f′(x)的图象都是连续不断的曲线,且对于实数a,b(a<b),有f'(a)>0,f′(b)<0,说明在区间(a,b)内存在x0,使f′(x0)=0,
所以函数f(x)在区间(a,b)内有极大值点,同时说明函数在区间[a,b]内至少有一个增区间和一个减区间.
由上面的分析可知,函数f(x)在区间[a,b]上不一定有零点,故①不正确;
因为函数在区间(a,b)内有极大值点,与实数b在同一个减区间内的极大值点的横坐标就是存在的一个x0,所以②正确;
函数f(x)在区间[a,b]的两个端点处的函数值无法判断大小,若f(b)>f(a),取x0=a,则③不正确;
当f(a)>f(b),且x0是极大值点的横坐标时结论④正确.
故选B.1年前查看全部
- 若函数f(x)的导函数f′(x)=x2-4x+3,则使得函数f(x+1)单调递减的一个充分不必要条件是x∈( )
若函数f(x)的导函数f′(x)=x2-4x+3,则使得函数f(x+1)单调递减的一个充分不必要条件是x∈( )
A. (0,1)
B. [0,2]
C. (1,3)
D. (2,4) 星星点灯6861年前2
星星点灯6861年前2 -
 三千胡杨 共回答了15个问题
三千胡杨 共回答了15个问题 |采纳率80%解题思路:由f′(x)=x2-4x+3≤0可解得x∈[1,3]为f(x)的减区间,从而有f(x+1)的单调递减区间为[0,2],再由集合法判断逻辑条件.由f′(x)=x2-4x+3≤0
得1≤x≤3
∴[1,3]为f(x)的减区间,
∴f(x+1)的单调递减区间为[0,2],
∵(0,1)⊆[0,2],
∴A选项是充分不必要条件
故选A.点评:
本题考点: 利用导数研究函数的单调性.
考点点评: 本题主要考查导数法研究函数的单调性,基本思路是:当函数是增函数时,导数大于等于零恒成立,当函数是减函数时,导数小于等于零恒成立.1年前查看全部
- 已知函数f(x)(x∈R)导函数f′(x)满足f′(x)<f(x),则当a>0时,f(a)与eaf(0)之间的大小关系为
已知函数f(x)(x∈R)导函数f′(x)满足f′(x)<f(x),则当a>0时,f(a)与eaf(0)之间的大小关系为( )
A.f(a)<eaf(0)
B.f(a)>eaf(0)
C.f(a)=eaf(0)
D.不能确定,与f(x)或a有关 jwt12191年前1
jwt12191年前1 -
 z574928096 共回答了16个问题
z574928096 共回答了16个问题 |采纳率100%解题思路:设函数f(x)=e
,则导函数f′(x)=[1/2]•ex 2
,显然满足f'(x)<f(x),x 2
由f(a)=e
,eaf(0)=ea,比较得出结论.a 2 由题意知,可设函数f(x)=e
x
2,则导函数f′(x)=[1/2]•e
x
2,显然满足f'(x)<f(x),
f(a)=e
a
2,eaf(0)=ea,当a>0时,显然 e
a
2<ea ,即f(a)<eaf(0),
故选 A.点评:
本题考点: 不等式比较大小.
考点点评: 本题考查求复合函数的导数的方法,以及指数函数的单调性.1年前查看全部
- (8214•大连二模)设函数f(x)是连续函数,且在x=1处存在导数.三函数f(x)及其导函数f′(x)满足f′(x)•
(8214•大连二模)设函数f(x)是连续函数,且在x=1处存在导数.三函数f(x)及其导函数f′(x)满足f′(x)•lnx=x-
,则函数f(x)( )f(x) x
A.既有极大值,又有极小值
B.有极大值,无极小值
C.有极小值,无极大值
D.既没有极大值,又没有极小值 slac1231年前1
slac1231年前1 -
 gozxf 共回答了24个问题
gozxf 共回答了24个问题 |采纳率91.7%解题思路:由f′(x)•lnx=x-
,由于(f(x)lnx)′=f′(x)lnx+f(x) x
,可得f(x)=f(x) x
,当x≠1时,f′(x)=1,x=1
,x>0且x≠1x2−1 2lnx
.令g(x)=2x2lnx-x2+1,可得g′(x)=4xlnx.利用其单调性可得:当x=1时,g(x)取得极小值即最小值,g(1)=0.进而得出函数f(x)的单调性.2x2lnx−(x2−1) 2xln2x 由f′(x)•lnx=x-f(x)x,∵(f(x)lnx)′=f′(x)lnx+f(x)x,∴(f(x)lnx)′=x,∴f(x)lnx=小2x2+c,(*)∵函数f(x)是连续函数,∴由f′(x)•lnx=x-f(x)x,可得f(小)=小,代入(*),可得c=-小2.∴f...
点评:
本题考点: 利用导数研究函数的极值.
考点点评: 本题考查了构造函数法利用导数求函数的解析式、利用导数研究函数的单调性极值与最值,考查了推理能力和计算能力,属于难题.1年前查看全部
- (2011•三亚模拟)定义域为R的函数f(x)对任意x都有f(2+x)=f(2-x),且其导函数f′(x)满足f′(x)
(2011•三亚模拟)定义域为R的函数f(x)对任意x都有f(2+x)=f(2-x),且其导函数f′(x)满足
>0,则当2<a<4,有( )f′(x) 2−x
A.f(2a)<f(log2a)<f(2)
B.f(log2a)<f(2)<f(2a)
C.f(2a)<f(2)<f(log2a)
D.f(log2a)<f(2a)<f(2) hudeli1年前1
hudeli1年前1 -
 makesunm 共回答了22个问题
makesunm 共回答了22个问题 |采纳率77.3%解题思路:先根据条件求出函数的对称轴,再求出函数的单调区间,然后判定2、log2a、2a的大小关系,根据单调性比较f(2)、f(log2a)、f(2a)的大小即可.∵函数f(x)对任意x都有f(2+x)=f(2-x),
∴函数f(x)的对称轴为x=2
∵导函数f′(x)满足
f′(x)
2−x>0,
∴函数f(x)在(2,+∞)上单调递减,(-∞,2)上单调递增,
∵2<a<4
∴1<log2a<2<4<2a
又函数f(x)的对称轴为x=2
∴f(2)>f(log2a)>f(2a),
故选A.点评:
本题考点: 函数的单调性与导数的关系;函数单调性的性质;奇偶函数图象的对称性.
考点点评: 本题主要考查了导数的运算,以及奇偶函数图象的对称性和比较大小,根据函数导函数的符号确定函数的单调区间是解决此题的关键,根据函数的单调性比较函数值的大小,属于基础题.1年前查看全部
- 给出定义:若函数f(x)在D上可导,即f′(x)存在,且导函数f′(x)在D上也可导,则称f(x)在D上存在二阶导函数,
给出定义:若函数f(x)在D上可导,即f′(x)存在,且导函数f′(x)在D上也可导,则称f(x)在D上存在二阶导函数,记f′(x)=(f′(x))′.若f″(x)<0在D上恒成立,则称f(x)在D上为凸函数.以下四个函数在(0,
)上不是凸函数的是______.(把你认为正确的序号都填上)π 2
①f(x)=sin x+cos x;
②f(x)=ln x-2x;
③f(x)=-x 3 +2x-1;
④f(x)=xe x . 刹那云开1年前1
刹那云开1年前1 -
 chemwinliu 共回答了21个问题
chemwinliu 共回答了21个问题 |采纳率100%对于①,f″(x)=-(sinx+cosx),x∈(0,
π
2 )时,
f″(x)<0恒成立;
对于②,f″(x)=-
1
x 2 ,在x∈(0,
π
2 )时,f″(x)<0恒成立;
对于③,f″(x)=-6x,在x∈(0,
π
2 )时,f″(x)<0恒成立;
对于④,f″(x)=(2+x)•e x 在x∈(0,
π
2 )时f″(x)>0恒成立,
所以f(x)=xe x 不是凸函数.
故答案为:④1年前查看全部
- (2011•汕头模拟)已知函数f(x)(x∈R)满足f(1)=1,且f′(x)的导函数f′(x)<12,则f(x)<x2
(2011•汕头模拟)已知函数f(x)(x∈R)满足f(1)=1,且f′(x)的导函数f′(x)<
,则f(x)<1 2
+x 2
的解集为( )1 2
A.{x|-1<x<1}
B.{x|x<-1}
C.{x|x<-1或x>1}
D.{x|x>1} 杜义军1年前1
杜义军1年前1 -
 lippyman 共回答了23个问题
lippyman 共回答了23个问题 |采纳率78.3%解题思路:先把不等式f(x)<
+x 2
移项并设φ(x)=f(x)-[x/2]-[1/2],然后求出导函数φ′(x)又因为函数f′(x)<1 2
,所以φ′(x)<0即φ(x)是减函数由f(1)=1求出φ(1)=0,根据函数是减函数得到f(x)<1 2
+x 2
的解集即可.1 2 ϕ(x)=f(x)−
x
2−
1
2,则ϕ/(x)=f/(x)−
1
2<0,
∴φ(x)在R上是减函数.
ϕ(1)=f(1)−
1
2−
1
2=1−1=0,
∴ϕ(x)=f(x)−
x
2−
1
2<0的解集为{x|x>1}.
故选D.点评:
本题考点: 函数单调性的性质;导数的运算;其他不等式的解法.
考点点评: 此题考查了导数的运算,函数单调性的应用,以及利用导数研究函数的增减性.1年前查看全部
- (2012•安徽模拟)设函数F(x)=f(x)ex是定义在R上的函数,其中f(x)的导函数f′(x)满足f′(x)<f(
(2012•安徽模拟)设函数F(x)=
是定义在R上的函数,其中f(x)的导函数f′(x)满足f′(x)<f(x)对于x∈R恒成立,则( )f(x) ex
A.f(2)>e2f(0),f(2012)>e2012f(0)
B.f(2)<e2f(0),f(2012)<e2012f(0)
C.f(2)>e2f(0),f(2012)<e2012f(0)
D.f(2)<e2f(0),f(2012)>e2012f(0) zhang110qi1年前1
zhang110qi1年前1 -
 0507211140 共回答了13个问题
0507211140 共回答了13个问题 |采纳率100%解题思路:根据函数F(x)=
的导数为F′(x)<0,可得函数F(x)=f(x) ex
是定义在R上的减函数,故有F(2)f(x) ex
<F(0),推出f(2)<e2f(0).同理可得f(2012)<e2012f(0),从而得出结论.函数F(x)=
f(x)
ex的导数为F′(x)=
f′(x)ex−f(x)ex
(ex)2=
f′(x)−f(x)
ex<0,
故函数F(x)=
f(x)
ex是定义在R上的减函数,
∴F(2)<F(0),即
f(2)
e2<
f(0)
e0,故有f(2)<e2f(0).
同理可得f(2012)<e2012f(0).
故选B.点评:
本题考点: 利用导数研究函数的单调性.
考点点评: 本题主要考查利用导数研究函数的单调性,导数的运算法则的应用,属于中档题.1年前查看全部
- 已知f(x)=x3+ax2+bx+c在x=1处的切线与直线x+2y-2=0互相垂直,且导函数f′(x)的图象关于直线x=
已知f(x)=x3+ax2+bx+c在x=1处的切线与直线x+2y-2=0互相垂直,且导函数f′(x)的图象关于直线x=
对称.1 3
(1)求a,b的值;
(2)若f(x)的图象与g(x)=x2的图象有且仅有三个公共点,求c的取值范围. 夕阳心情的母亲1年前0
夕阳心情的母亲1年前0 -
 共回答了个问题
共回答了个问题 |采纳率
- (2014•丽水二模)函数f(x)的导函数f′(x)的图象是如图所示的一条直线l,l与x轴交点坐标为(1,0),若|a-
 (2014•丽水二模)函数f(x)的导函数f′(x)的图象是如图所示的一条直线l,l与x轴交点坐标为(1,0),若|a-1|<|b-1|,则f(a)与f(b)的大小关系为( )
(2014•丽水二模)函数f(x)的导函数f′(x)的图象是如图所示的一条直线l,l与x轴交点坐标为(1,0),若|a-1|<|b-1|,则f(a)与f(b)的大小关系为( )
A.f(a)>f(b)
B.f(a)<f(b)
C.f(a)=f(b)
D.无法确定 白天加班1年前1
白天加班1年前1 -
 韶晖 共回答了17个问题
韶晖 共回答了17个问题 |采纳率76.5%解题思路:由导函数的图象是一条直线,知道原函数是二次函数,再根据导数的正负性,得出对称轴和开口方向,由二次函数的性质即可得出答案.由f′(x)图象为一直线l,知f(x)是一个二次函数,
又∵当x∈(-∞,1)时f′(x)>0,f(x)单调递增,当x∈(1,+∞)时,f′(x)<0,f(x)单调递减;
∴f(x)的对称轴为x=1,且抛物线的开口向下,
又∵|a-1|<|b-1|,
∴a与对称轴较近,
∴f(a)>f(b).
故选:A.点评:
本题考点: 利用导数研究函数的单调性.
考点点评: 本题考查了函数与导数的性质,二次函数的性质特点,属于基础题.1年前查看全部
- 函数y=f(x)在区间(0,+∞)内可导,导函数f′(x)是减函数,且f′(x)>0.设x0∈(0,+∞),y=kx+m
函数y=f(x)在区间(0,+∞)内可导,导函数f′(x)是减函数,且f′(x)>0.设x0∈(0,+∞),y=kx+m是曲线y=f(x)在点(x0,f(x0))得的切线方程,并设函数g(x)=kx+m.
(1)用x0、f(x0)、f′(x0)表示m;
(2)证明:当x0∈(0,+∞)时,g(x)≥f(x).
 飞呀飞飞111年前2
飞呀飞飞111年前2 -
 powerstj 共回答了14个问题
powerstj 共回答了14个问题 |采纳率92.9%解题思路:(I)先利用点斜式表示出切线方程,然后根据切线方程与y=kx+m是同一直线建立等式关系,求出m即可;
(II)比较g(x)与f(x)的大小可利用作差比较,构造函数h(x)=g(x)-f(x),然后利用导数研究函数h(x)的单调性,求出函数h(x)的最小值,即可证得结论.(Ⅰ) y-f(x0)=f'(x0)(x-x0)
∴m=f(x0)-x0f'(x0).
(Ⅱ)证明:令h(x)=g(x)-f(x),则h'(x)=f'(x0)-f'(x),h'(x0)=0.
因为f'(x)递减,所以h'(x)递增,因此,当x>x0时,h'(x)>0;
当x<x0时,h'(x)<0.所以x0是h(x)唯一的极值点,且是极小值点,
可知h(x)的最小值为0,因此h(x)≥0,即g(x)≥f(x).点评:
本题考点: 利用导数研究函数的单调性.
考点点评: 本题主要考查了利用导数研究函数的单调性,以及比较两函数的大小,比较大小常常运用作差法进行比较,属于中档题.1年前查看全部
- (2014•鄂州模拟)函数f(x)的导函数f′(x)的图象是如图所示的一条直线l,l与x轴交点的坐标为(1,0),则f(
 (2014•鄂州模拟)函数f(x)的导函数f′(x)的图象是如图所示的一条直线l,l与x轴交点的坐标为(1,0),则f(0)和f(3)的大小关系为( )
(2014•鄂州模拟)函数f(x)的导函数f′(x)的图象是如图所示的一条直线l,l与x轴交点的坐标为(1,0),则f(0)和f(3)的大小关系为( )
A.f(0)<f(3)
B.f(0)>f(3)
C.f(0)=f(3)
D.不能确定 litchituli1年前1
litchituli1年前1 -
 夜莺与玫瑰 共回答了21个问题
夜莺与玫瑰 共回答了21个问题 |采纳率90.5%解题思路:根据导函数的图象,写出函数f(x)的单调区间,由导函数图象是一条直线知原函数是二次函数,对称轴是x=1,从而将f(0),f(3)转换到单调区间,就能比较大小了.由导函数f′(x)的图象可知:
函数f(x)的增区间为(-∞,1),减区间为(1,+∞),
又导函数f′(x)的图象是一条直线l,
∴原函数是二次项系数小于0的二次函数,其图象的对称轴是x=1.
∴f(x)=f(2-x),∴f(0)=f(2),
由函数f(x)在(1,+∞)上是减函数,
得f(2)>f(3),即f(0)>f(3).
故选B.点评:
本题考点: 利用导数研究函数的单调性.
考点点评: 本题主要考查利用导数研究函数的性质:单调性,进而比较两数大小,解题时应注意导函数的图象与原函数的关系是解决问题的关键.1年前查看全部
- 已知可导函数f(x)(x∈R)的导数f'(x)满足f'(x)>f(x),则不等ef(x)>f(1)e^x的解集是
 堂堂山枣1年前1
堂堂山枣1年前1 -
 jingzi0901 共回答了12个问题
jingzi0901 共回答了12个问题 |采纳率100%令g(x)=f(x)/e^x
则g'(x)=(f'(x)e^x-f(x)e^x)/e^(2x)=(f'(x)-f(x))/e^x>0
所以g单增
所以g(x)>g(1)(即原不等式)的解集是(1,+∞)1年前查看全部
- 若函数f(x)=kax-a-x(a>0且a≠1)在(-∞,+∞)上既是奇函数又是增函数,则其导函数f′(x)的图象可能是
若函数f(x)=kax-a-x(a>0且a≠1)在(-∞,+∞)上既是奇函数又是增函数,则其导函数f′(x)的图象可能是( )
A.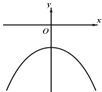
B.
C.
D.
 asp蓉1年前1
asp蓉1年前1 -
 斯特拉迪 共回答了20个问题
斯特拉迪 共回答了20个问题 |采纳率80%解题思路:由奇函数和增函数的性质可得k=1,a>1,进而可得函数的解析式,求导后综合研究选项可得答案.∵函数f(x)=kax-a-x,(a>0且a≠1)在(-∞,+∞)上是奇函数则f(-x)+f(x)=0,即ka-x-ax+kax-a-x=0,故(k-1)(ax-a-x)=0,解得k=1,又∵函数f(x)=kax-a-x,(a>0,a≠1)在(-∞,+∞)上是增函数,所...
点评:
本题考点: 函数的单调性与导数的关系;函数的图象;导数的运算.
考点点评: 本题考查函数的奇偶性和单调性,涉及导数和函数的图象,属中档题.1年前查看全部
- 设函数f(x)定义在(0,+∞)上,f(1)=0,导函数f′(x)= 1 x ,g(x)=f(x)+f′(x).
设函数f(x)定义在(0,+∞)上,f(1)=0,导函数f′(x)=
,g(x)=f(x)+f′(x).1 x
(Ⅰ)求g(x)的单调区间和最小值;
(Ⅱ)讨论g(x)与 g(
) 的大小关系;1 x
(Ⅲ)是否存在x 0 >0,使得|g(x)-g(x 0 )|<
对任意x>0成立?若存在,求出x 0 的取值范围;若不存在请说明理由.1 x  蓝尐伊1年前1
蓝尐伊1年前1 -
 jjpabcd 共回答了20个问题
jjpabcd 共回答了20个问题 |采纳率95%(Ⅰ)由题设易知f(x)=lnx,g(x)=lnx+
1
x ,
∴g′(x)=
x-1
x 2 ,令g′(x)=0,得x=1,
当x∈(0,1)时,g′(x)<0,故g(x)的单调递减区间是(0,1),
当x∈(1,+∞)时,g′(x)>0,故g(x)的单调递增区间是(1,+∞),
因此x=1是g(x)的唯一极值点,且为极小值点,从而是最小值点,
∴最小值为g(1)=1;
(Ⅱ) g(
1
x ) =-lnx+x,
设h(x)=g(x)- g(
1
x ) =2lnx-x+
1
x ,
则h′(x)= -
(x-1) 2
x 2 ,
当x=1时,h(1)=0,即g(x)= g(
1
x ) ,
当x∈(0,1)∪(1,+∞)时,h′(x)<0,h′(1)=0,
因此,h(x)在(0,+∞)内单调递减,
当0<x<1,时,h(x)>h(1)=0,即g(x)> g(
1
x ) ,
当x>1,时,h(x)<h(1)=0,即g(x)< g(
1
x ) ,
(Ⅲ)满足条件的x 0 不存在.证明如下:证法一 假设存在x 0 >0,
使|g(x)-g(x 0 )|<
1
x 成立,即对任意x>0,
有 Inx<g( x 0 )<Inx+
2
x ,(*)但对上述x 0 ,取 x 1 = e g( x 0 ) 时,
有 Inx 1 =g(x 0 ),这与(*)左边不等式矛盾,
因此,不存在x 0 >0,使|g(x)-g(x 0 )|<
1
x 成立.
证法二 假设存在x 0 >0,使|g(x)-g(x 0 )|成<
1
x 立.
由(Ⅰ)知, e g( x 0 ) 的最小值为g(x)=1.
又 g(x)=Inx+
1
x >Inx,
而x>1 时,Inx 的值域为(0,+∞),
∴x≥1 时,g(x) 的值域为[1,+∞),从而可取一个x 1 >1,
使 g(x 1 )≥g(x 0 )+1,即g(x 1 )-g(x 0 )≥1,
故|g(x 1 )-g(x 0 )|≥1>
1
x 1 ,与假设矛盾.
∴不存在x 0 >0,使|g(x)-g(x 0 )|<
1
x 成立.1年前查看全部
- 设函数f(x)=x m +ax的导函数f′(x)=2x+1,则 ∫ 21 f(-x)dx的值等于( ) A. 5 6
设函数f(x)=x m +ax的导函数f′(x)=2x+1,则
f(-x)dx的值等于( )∫ 21 A. 5 6 B. 1 2 C. 2 3 D. 1 6  douglas11281年前1
douglas11281年前1 -
 们面15对 共回答了18个问题
们面15对 共回答了18个问题 |采纳率100%由于f(x)=x m +ax的导函数f′(x)=2x+1,
∴f(x)=x 2 +x,
于是∫ 1 2 f(-x)dx=∫ 1 2 (x 2 -x)dx
=(
1
3 x 3 -
1
2 x 2 )| 1 2 =
5
6 .
故选A.1年前查看全部
- 已知函数f(x)=logax(0<a<1)的导函数f′(x),A=f′(a),b=f(a+1)-f(a),C=f′(a+
已知函数f(x)=logax(0<a<1)的导函数f′(x),A=f′(a),b=f(a+1)-f(a),C=f′(a+1),D=f(a+2)-f(a+1),则A,B,C,D中最大的数是( )
A. A
B. B
C. C
D. D 509522031年前0
509522031年前0 -
 共回答了个问题
共回答了个问题 |采纳率
- 已知函数f(x)的导函数f′(x)=2x-9,且f(0)的值为整数,当x∈(n,n+1](n∈N*)时,f(x)的值为整
已知函数f(x)的导函数f′(x)=2x-9,且f(0)的值为整数,当x∈(n,n+1](n∈N*)时,f(x)的值为整数的个数有且只有1个,则n= ___ .
 克淋顿1年前1
克淋顿1年前1 -
 hbzjc 共回答了20个问题
hbzjc 共回答了20个问题 |采纳率80%解题思路:因为f'(x)=2x-9,所以可设f(x)=x2-9x+k,则f(0)=k为整数,由于n为正整数,可得f(n+1)及f(n)均为整数,函数的对称轴为x=4.5,利用函数的最大值与最小值的差,可得结论.因为f′(x)=2x-9,所以可设f(x)=x2-9x+k,
由f(0)=k,k为整数,n为正整数,可得f(n+1)及f(n)均为整数.
配方可得f(x)=x2-9x+k=(x-4.5)2-4.52+k,为开口向上的二次函数,对称轴为x=4.5
当x∈(4,5]时,f(x)max-f(x)min=f(5)-f(4.5)=0.25,
又f(5)=-20+k∈Z,故只有1个整数f(5).
即当x∈(4,5]时,f(x)的值为整数的个数有且只有1个
故答案为:4点评:
本题考点: 导数的运算;根的存在性及根的个数判断.
考点点评: 本题考查导数知识的运用,考查函数解析式的运用,属于基础题.1年前查看全部
- 已知定义在R上的函数f(x)满足f(2)=1,且f(x)的导函数f′(x)>x-1,则不等式f(x)<[1/2]x2-x
已知定义在R上的函数f(x)满足f(2)=1,且f(x)的导函数f′(x)>x-1,则不等式f(x)<[1/2]x2-x+1的解集为( )
A. {x|-2<x<2}
B. {x|x>2}
C. {x|x<2}
D. {x|x<-2或x>2} kidhippo1年前1
kidhippo1年前1 -
 nba1981 共回答了19个问题
nba1981 共回答了19个问题 |采纳率89.5%解题思路:通过对题目的分析,可构造函数g(x)=f(x)-
x2+x,利用函数g(x)的单调性即可解出.1 2 令g(x)=f(x)-
1
2x2+x,对g(x)求导,得g′(x)=f′(x)-x+1,
∵f′(x)>x-1,∴g′(x)>0,即g(x)在R上为增函数.
不等式f(x)<
1
2x2-x+1可化为f(x)-
1
2x2+x<1,即g(x)<g(2),
由g(x)单调递增得x<2,所以不等式的解集为{x|x<2}.
故选C.点评:
本题考点: 利用导数研究函数的单调性.
考点点评: 本题考查了灵活利用导数研究函数的单调性以及抽象不等式的解法,据已知恰当构造函数是解决本题的关键.1年前查看全部
- 已知函数f(x)的导函数f′(x)=a(x+1)(x-a),若f(x)在x=a处取到极小值,则实数a的取值范围是____
已知函数f(x)的导函数f′(x)=a(x+1)(x-a),若f(x)在x=a处取到极小值,则实数a的取值范围是______.
 清茶sy1年前4
清茶sy1年前4 -
 百箭 共回答了21个问题
百箭 共回答了21个问题 |采纳率85.7%解题思路:根据函数导数的定义和性质即可得到结论.由f′(x)=a(x+1)(x-a)=0,
解得a=0或x=-1或x=a,
若a=0,则f′(x)=0,此时函数f(x)为常数,没有极值,故a≠0.
若a=-1,则f′(x)=-(x+1)2≤0,此时函数f(x)单调递减,没有极值,故a≠-1.
若a<-1,由f′(x)=a(x+1)(x-a)>0得a<x<-1此时函数单调递增,
由f′(x)=a(x+1)(x-a)<0得x<a或x>-1此时函数单调递减,即函数在x=a处取到极小值,满足条件.
若-1<a<0,由f′(x)=a(x+1)(x-a)>0得-1<x<a此时函数单调递增,
由f′(x)=a(x+1)(x-a)<0得x<-1或x>a,此时函数单调递减,即函数在x=a处取到极大值,不满足条件.
若a>0,由f′(x)=a(x+1)(x-a)>0得x<-1或x>a此时函数单调递增,
由f′(x)=a(x+1)(x-a)<0得-1<x<a,此时函数单调递减,即函数在x=a处取到极小值,满足条件.
综上:a<-1或a>0,
故答案为:a<-1或a>0点评:
本题考点: 函数在某点取得极值的条件.
考点点评: 本题主要考查导数和极值的关系,利用二次函数的图象和性质是解决本题的关键.1年前查看全部
- 在下面四个图中,有一个是函数f(x)=[1/3x3+ax2+(a2−1)x+1(a∈R,a≠0)的导函数f′(x)的图象
在下面四个图中,有一个是函数f(x)=[1/3x3+ax2+(a2−1)x+1
 紫衣tracy1年前1
紫衣tracy1年前1 -
 润仔123 共回答了19个问题
润仔123 共回答了19个问题 |采纳率84.2%解题思路:求出导函数,据导函数的二次项系数为正得到图象开口向上;利用函数解析式中有2ax,故函数不是偶函数,得到函数的图象.∵f′(x)=x2+2ax+(a2-1),
∴导函数f′(x)的图象开口向上.
又∵a≠0,
∴f′(x)不是偶函数,其图象不关于y轴对称
其图象必为第四张图.由图象特征知f′(0)=0,∴a2-1=0,
且对称轴-a>0,
∴a=-1.
∴函数f(x)=[1/3]x3-x2+1,
故答案为f(-1)=-[1/3]-1+1=-[1/3],
故选:B.点评:
本题考点: 函数的图象;导数的运算.
考点点评: 本题考查函数与其导函数的综合应用,三次函数与其导函数(二次函数)的关系,综合考查二次函数的应用.1年前查看全部
- 函数f(x)(x∈R)满足f(1)=1,且f(x)在R上的导函数f′(x)>[1/2],则不等式f(lnx)<[1+ln
函数f(x)(x∈R)满足f(1)=1,且f(x)在R上的导函数f′(x)>[1/2],则不等式f(lnx)<[1+lnx/2]的解集为______.
 y6m7gd1年前1
y6m7gd1年前1 -
 一网打尽888 共回答了17个问题
一网打尽888 共回答了17个问题 |采纳率94.1%解题思路:设g(lnx)=f(lnx)-[1+lnx/2],得出g(x)在R上是增函数,且g(1)=0.所以f(lnx)<[1+lnx/2]的解集即是g(lnx)<0=g(1)的解集,解出即可.设g(lnx)=f(lnx)-[1+lnx/2],
∵f(1)=1,f'(x)>[1/2],
∴g(1)=f(1)-1=0,g′(x)=f′(x)-[1/2]>0,
∴g(x)在R上是增函数,且g(1)=0.
令t=lnx(t>0),则g(t)=f(t)-[1+t/2],
∴f(t)<[1+t/2]的解集即是g(t)<0=g(1)的解集.
∴t<1即lnx<1,
∴0<x<e,
故答案为:(0,e).点评:
本题考点: 利用导数研究函数的单调性.
考点点评: 本题考查了函数的单调性,导数的应用,对数函数的性质,考查转化思想,是一道中档题.1年前查看全部
- 已知f(x)=1/2x-cosx,x∈[-1.1]则导函数f′(x)是
 llj0981年前1
llj0981年前1 -
 花样人 共回答了13个问题
花样人 共回答了13个问题 |采纳率100%X+sinx1年前查看全部
- 已知f(x)=12x2−cosx,x∈[−1,1],则导函数f′(x)是( )
已知f(x)=
x2−cosx,x∈[−1,1],则导函数f′(x)是( )1 2
A. 仅有最小值的奇函数
B. 既有最大值,又有最小值的偶函数
C. 仅有最大值的偶函数
D. 既有最大值,又有最小值的奇函数 西元龙卷风1年前1
西元龙卷风1年前1 -
 redstair 共回答了18个问题
redstair 共回答了18个问题 |采纳率94.4%解题思路:求出f′(x),利用导数可判断其单调性,通过单调性即可求出其最大最小值;再用定义可判断其奇偶性,从而得出答案.f′(x)=x+sinx,令g(x)=x+sinx,则g′(x)=1+cosx.
当x∈[-1,1]时,g′(x)>0,所以f′(x)=g(x)在[-1,1]上单调递增,
所以f′(-1)≤f′(x)≤f′(1),即-1-sin1≤f′(x)≤1+sin1.
又f′(-x)=-x+sin(-x)=-x-sinx=-(x+sinx)=-f′(x),所以f′(x)是奇函数.
故选D.点评:
本题考点: 利用导数求闭区间上函数的最值.
考点点评: 本题考查了应用导数求函数最值问题,奇偶性的判断,难度不大.掌握相关基础知识是解决该题的关键.1年前查看全部
- (2013•河池模拟)已知函数f(x)的导函数f′(x)的图象如图所示,那么函数f(x)的图象最有可能的是( )
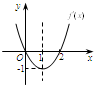 (2013•河池模拟)已知函数f(x)的导函数f′(x)的图象如图所示,那么函数f(x)的图象最有可能的是( )
(2013•河池模拟)已知函数f(x)的导函数f′(x)的图象如图所示,那么函数f(x)的图象最有可能的是( )
A.
B.
C.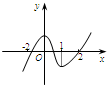
D.
 ageheh1年前1
ageheh1年前1 -
 不哭的tt 共回答了20个问题
不哭的tt 共回答了20个问题 |采纳率85%解题思路:根据导函数图象可知,函数在(-∞,0),(2,+∞)上单调增,在(0,2)上单调减,从而可得结论.根据导函数图象可知,函数在(-∞,0),(2,+∞)上单调增,在(0,2)上单调减,由此可知函数f(x)的图象最有可能的是A
故选A.点评:
本题考点: 利用导数研究函数的单调性.
考点点评: 本题考查导函数与原函数图象的关系,解题的关键是利用导函数看正负,原函数看增减,属于基础题.1年前查看全部
- (2013•醴陵市模拟)已知二次函数f(x)的图象如图所示,则其导函数f′(x)的图象大致形状是( )
(2013•醴陵市模拟)已知二次函数f(x)的图象如图所示,则其导函数f′(x)的图象大致形状是( )

A.
B.
C.
D.
 hatetime1年前1
hatetime1年前1 -
 撒嘎 共回答了19个问题
撒嘎 共回答了19个问题 |采纳率84.2%解题思路:先根据图象可知二次函数的二次项系数为负,由于对称轴为y轴可知一次项系数为0,然后写出它的导函数即可直接判断.∵二次函数的图象开口向下
∴二次函数的二次项系数为负,
∵对称轴为y轴
∴一次项系数为0,
设其为y=ax2+c,且a<0,
∴y′=-2ax,且a<0,过原点与第二四象限;
故答案为B.点评:
本题考点: 函数的图象;导数的几何意义.
考点点评: 本题考查了根据图象写出函数式的知识和导函数的写法.1年前查看全部
- 给出定义:若函数f(x)在D上可导,即f′(x)存在,且导函数f′(x)在D上也可导,则称f(x)在D上存在二阶导函数,
给出定义:若函数f(x)在D上可导,即f′(x)存在,且导函数f′(x)在D上也可导,则称f(x)在D上存在二阶导函数,记f″(x)=(f′(x))′,若f″(x)<0在D上恒成立,则称f(x)在D上为凸函数.以下四个函数在 (0,
) 上不是凸函数的是( )π 2 A.f(x)=sinx+cosx B.f(x)=lnx-2x C.f(x)=-x 3 +2x-1 D.f(x)=-xe -x  61029391年前1
61029391年前1 -
 wghit 共回答了16个问题
wghit 共回答了16个问题 |采纳率87.5%对于f(x)=sinx+cosx,f′(x)=cosx-sinx,f″(x)=-sinx-cosx,当x∈ (0,
π
2 ) 时,f″(x)<0,故为凸函数,排除A;
对于f(x)=lnx-2x,f′(x)=
1
x -2 ,f″(x)=-
1
x 2 ,当x∈ (0,
π
2 ) 时,f″(x)<0,故为凸函数,排除B;
对于f(x)=-x 3 +2x-1,f′(x)=-3x 2 +2,f″(x)=-6x,当x∈ (0,
π
2 ) 时,f″(x)<0,故为凸函数,排除C;
故选D.1年前查看全部
- 已知函数f(x)=ax3+bx(a≠0)的图象在点(1,f(1))处的切线斜率为-6,其导函数f′(x)的最小值为-12
已知函数f(x)=ax3+bx(a≠0)的图象在点(1,f(1))处的切线斜率为-6,其导函数f′(x)的最小值为-12.
(1)求a,b的值.
(2)求函数f(x)的单调递增区间. angel5001年前1
angel5001年前1 -
 chengbainan 共回答了19个问题
chengbainan 共回答了19个问题 |采纳率94.7%解题思路:(1)先根据导函数f'(x)的最小值求出b的值,最后依据在x=1处的导数等于切线的斜率求出c的值即可;
(2)先求导数fˊ(x),在函数的定义域内解不等式fˊ(x)>0,求得区间即为单调增区间.(1)∵函数f(x)=ax3+bx,f'(x)=3ax2+b
∵f(x)在点(1,f(1))处的切线切线斜率为-6,
∴f′(1)=-6,即3a+b=-6 …①
又∵导函数f'(x)的最小值为-12,∴a>0且b=-12 …②
由①②解出a=2,b=-12,∴f(x)=2x3-12x …(6分)
(2)∵f′(x)=6x2-12=6(x+
2)(x-
2)
∴令f′(x)>0,得x∈(-∞,-
2)∪(
2,+∞).
∴f函数f(x)的单调递增区间(-∞,-
2),(
2,+∞).点评:
本题考点: 利用导数研究曲线上某点切线方程;利用导数研究函数的单调性.
考点点评: 本题考查函数的单调性、二次函数的最值、导数的应用等基础知识,以及推理能力和运算能力.1年前查看全部
- 1.定义在R上的函数f(x)及其导函数f′(x)的图像都是连续不断的曲线,且对于实数a,b(a0,f′(b)f(b);
1.定义在R上的函数f(x)及其导函数f′(x)的图像都是连续不断的曲线,且对于实数a,b(a0,f′(b)f(b);
(3)存在x.属于[a,b],f(x.) >=f(a); (4)存在x.属于[a,b],f(a)-f(b)>f′(x.)(a-b)
其中结论正确的个数是( ) A.1 个 B.2 个 C.3 个 D.4个 54hfc1年前1
54hfc1年前1 -
 鱼龙化石 共回答了12个问题
鱼龙化石 共回答了12个问题 |采纳率83.3%1错2对3对4对 C1年前查看全部
- 给出定义:若函数f(x)在D上可导,即f′(x)存在,且导函数f′(x)在D上也可导,则称f(x)在D上存在二阶导函数,
给出定义:若函数f(x)在D上可导,即f′(x)存在,且导函数f′(x)在D上也可导,则称f(x)在D上存在二阶导函数,记f″(x)=(f′(x))′.若f″(x)<0在D上恒成立,则称f(x)在D上为凸函数。以下四个函数在(0,  )上不是凸函数的是( )。(把你认为正确的序号都填上)
)上不是凸函数的是( )。(把你认为正确的序号都填上) pxynow1年前1
pxynow1年前1 -
 13最嗲啊 共回答了27个问题
13最嗲啊 共回答了27个问题 |采纳率92.6%④1年前查看全部
- 已知关于x的函数f(x)=−13x3 +bx2 +cx+bc,其导函数f′(x).
已知关于x的函数f(x)=−
1 3
+bx 3
+cx+bc,其导函数f′(x).x 2
(1)如果函数f(x)在x=1处有极值−
,试确定b、c的值;4 3
(2)设当x∈(0,1)时,函数y=f(x)-c(x+b)的图象上任一点P处的切线斜率为k,若k≤1,求实数b的取值范围. ajkevin1年前0
ajkevin1年前0 -
 共回答了个问题
共回答了个问题 |采纳率
- 设f″(x)是函数y=f(x)的导函数f′(x)的导数,定义:若f(x)=ax3+bx2+cx+d(a≠0),且方程f″
设f″(x)是函数y=f(x)的导函数f′(x)的导数,定义:若f(x)=ax3+bx2+cx+d(a≠0),且方程f″(x)=0有实数解x0,则称点(x0,f(x0))为函数y=f(x)的对称中心.有同学发现“任何一个三次函数都有对称中心”,请你运用这一发现处理下列问题:设g(x)=[1/3x3−
x2+3x−1 2 5 12],则
(1)函数g(x)的对称中心为([1/2],1)([1/2],1);
(2)g([1/2015])+g([2/2015])+g([3/2015])+…+g([2014/2015])=______.赞
lance_ibm 幼苗
共回答了18个问题采纳率:94.4% 举报
解题思路:(1)根据函数g(x)的解析式求出g′(x)和g″(x),令g″(x)=0,求得x的值,由此求得函数g(x)的对称中心.
(2)由导函数的导函数等于0求出x的值,可得g(x0)+f(1-x0)=y0+(2-y0)=2,从而得到g([1/2015])+g([2/2015])+g([3/2015])+…+g([2014/2015])的值.(1)∵g(x)=[1/3x3−
1
2x2+3x−
5
12],
又g′(x)=x2-x+3,g″(x)=2x-1,
令g″(x)=0得x=[1/2],∴g([1/2])=[1/3×(
1
2)3−
1
2×(
1
2)2+3×
1
2−
5
12]=1
故函数g(x)的对称中心为([1/2],1).
(2)设P(x0,y0)在g(x)上可知P关于对称点([1/2],1)的对称点g(1-x0,2-y0)也在函数g(x)上,
∴g(1-x0)=2-y0
∴g(x0)+g(1-x0)=y0+(2-y0)=2,
∵g([1/2015])+g([2/2015])+…+g([2014/2015])
=[g([1/2015])+g([2014/2015])]+…+[g([2007/2015])+g([2008/2015])]=2×1007=2014.点评:
本题考点: 导数的运算.
考点点评: 本小题主要考查函数与导数等知识,考查化归与转化的数学思想方法,考查化简计算能力,函数的对称性的应用,属于基础题.1年前
8可能相似的问题-
1年前1个回答
-
1年前1个回答
-
1年前1个回答
-
1年前3个回答
-
1年前2个回答
你能帮帮他们吗
Copyright © 2022 YULUCN.COM - 雨露学习互助 - 17 q. 0.050 s. - webmaster@yulucn.com 守护北半球1年前1
守护北半球1年前1 -
 lance_ibm 共回答了18个问题
lance_ibm 共回答了18个问题 |采纳率94.4%解题思路:(1)根据函数g(x)的解析式求出g′(x)和g″(x),令g″(x)=0,求得x的值,由此求得函数g(x)的对称中心.
(2)由导函数的导函数等于0求出x的值,可得g(x0)+f(1-x0)=y0+(2-y0)=2,从而得到g([1/2015])+g([2/2015])+g([3/2015])+…+g([2014/2015])的值.(1)∵g(x)=[1/3x3−
1
2x2+3x−
5
12],
又g′(x)=x2-x+3,g″(x)=2x-1,
令g″(x)=0得x=[1/2],∴g([1/2])=[1/3×(
1
2)3−
1
2×(
1
2)2+3×
1
2−
5
12]=1
故函数g(x)的对称中心为([1/2],1).
(2)设P(x0,y0)在g(x)上可知P关于对称点([1/2],1)的对称点g(1-x0,2-y0)也在函数g(x)上,
∴g(1-x0)=2-y0
∴g(x0)+g(1-x0)=y0+(2-y0)=2,
∵g([1/2015])+g([2/2015])+…+g([2014/2015])
=[g([1/2015])+g([2014/2015])]+…+[g([2007/2015])+g([2008/2015])]=2×1007=2014.点评:
本题考点: 导数的运算.
考点点评: 本小题主要考查函数与导数等知识,考查化归与转化的数学思想方法,考查化简计算能力,函数的对称性的应用,属于基础题.1年前查看全部
- 设函数f(x)=(2x+5)6,则导函数f′(x)中的x3的系数是______.
 看守在家1年前2
看守在家1年前2 -
 jolin722 共回答了19个问题
jolin722 共回答了19个问题 |采纳率94.7%解题思路:先求导函数,再结合二项式定理,表示出含有x3的项,从而求出x3的系数f′(x)=6(2x+5)5×2=12(2x+5)5
由二项式定理知,含有x3的项为:12×
C25•(2x)3•52=24000x3
故答案为:24000点评:
本题考点: 简单复合函数的导数;二项式定理.
考点点评: 本题考察复合函数求导和二项式定理的相关知识.注意复合函数求导时,要先求构成原函数的两个简单函数的导数,再相乘即可.属中档题1年前查看全部
- 下列图象中,有一个是函数f(x)=[1/3]x3+ax2+(a2-1)x+1(a∈R,a≠0)的导函数f′(x)的图象,
下列图象中,有一个是函数f(x)=[1/3]x3+ax2+(a2-1)x+1(a∈R,a≠0)的导函数f′(x)的图象,则f(-1)=-[1/3]-[1/3].

 jerrypigeon1年前1
jerrypigeon1年前1 -
 羽毛笔HOHO7怪a16 共回答了19个问题
羽毛笔HOHO7怪a16 共回答了19个问题 |采纳率100%解题思路:求出导函数,据导函数的二次项系数为正得到图象开口向上;利用函数解析式中有2ax,故函数不是偶函数,得到函数的图象.∵f′(x)=x2+2ax+(a2-1),
∴导函数f′(x)的图象开口向上.
又∵a≠0,
∴f(x)不是偶函数,其图象不关于y轴对称
其图象必为第三张图.由图象特征知f′(0)=0,
且对称轴-a>0,
∴a=-1.
故答案为f(-1)=-[1/3]-1+1=-[1/3].点评:
本题考点: 利用导数研究函数的单调性.
考点点评: 本题考查导函数的运算法则、二次函数的图象与二次函数系数的关系:开口方向与二次项系数的符号有关、
对称轴公式.1年前查看全部
- 已知函数f(x)=x3+ax2+2,若f(x)的导函数f′(x)的图象关于直线x=1对称.
已知函数f(x)=x3+ax2+2,若f(x)的导函数f′(x)的图象关于直线x=1对称.
(Ⅰ)求导函数f′(x)及实数a的值;
(Ⅱ)求函数y=f(x)在区间[-1,2]上的最大值和最小值. 超级食客1年前1
超级食客1年前1 -
 fly_hevin 共回答了20个问题
fly_hevin 共回答了20个问题 |采纳率85%解题思路:(Ⅰ)求出f′(x),由其图象关于x=1对称即可求出a值,从而得到f′(x).
(Ⅱ)借助(Ⅰ)问,求出f(x)在区间[-1,2]上的极值、端点处函数值,其中最大者为最大值,最小者为最小值.(Ⅰ)f′(x)=3x2+2ax,
因为f′(x)的图象关于直线x=1对称,所以-[1/3]a=1,a=-3,从而f′(x)=3x2-6x.
故f′(x)=3x2-6x,a=-3.
(Ⅱ)由(Ⅰ)知:f(x)=x3-3x2+2,f′(x)=3x(x-2),
则当x∈[-1,0)时,f′(x)>0,f(x)单调递增;当x∈(0,2)时,f′(x)<0,f(x)单调递减.
∴f(0)=2为极大值,又f(-1)=-2,f(2)=-2.
所以y=f(x)在区间[-1,2]上的最大值为2,最小值为-2.点评:
本题考点: 导数的运算;利用导数求闭区间上函数的最值.
考点点评: 本题考查应用导数求函数在闭区间上的最值问题,以及分析问题解决问题的能力.1年前查看全部
- (2011•桂林模拟)已知三次函数f(x)的导函数f′(x)=3x2-3ax,f(0)=b,a、b为实数.
(2011•桂林模拟)已知三次函数f(x)的导函数f′(x)=3x2-3ax,f(0)=b,a、b为实数.
(1)若曲线y=f(x)在点(a+1,f(a+1))处切线的斜率为12,求a的值;
(2)若f(x)在区间[-1,1]上的最小值、最大值分别为-2、1,且1<a<2,求函数f(x)的解析式. 如风走过1年前1
如风走过1年前1 -
 249595765 共回答了18个问题
249595765 共回答了18个问题 |采纳率88.9%解题思路:(1)求出x=a+1处的导数值即切线的斜率,令其为12,列出方程,求出a的值.
(2)据导函数的形式设出f(x),求出导函数为0的两个根,判断出根与定义域的关系,求出函数的最值,列出方程求出f(x)的解析式.(1)由导数的几何意义f′(a+1)=12
∴3(a+1)2-3a(a+1)=12
∴3a=9∴a=3
(2)∵f′(x)=3x2-3ax,f(0)=b
∴f(x)=x3−
3
2ax2+b
由f′(x)=3x(x-a)=0得x1=0,x2=a
∵x∈[-1,1],1<a<2
∴当x∈[-1,0)时,f′(x)>0,f(x)递增;当x∈(0,1]时,f′(x)<0,f(x)递减.
∴f(x)在区间[-1,1]上的最大值为f(0)
∵f(0)=b,
∴b=1
∵f(1)=1−
3
2a+1=2−
3
2a,f(−1)=−1−
3
2a+1=−
3
2a
∴f(-1)<f(1)
∴f(-1)是函数f(x)的最小值,
∴−
3
2a=−2
∴a=
4
3
∴f(x)=x3-2x2+1点评:
本题考点: 利用导数求闭区间上函数的最值;函数解析式的求解及常用方法;导数的运算.
考点点评: 曲线在切点处的导数值为曲线的切线斜率;求函数的最值,一定要注意导数为0的根与定义域的关系.1年前查看全部
- 已知可导函数f(x)(x∈R)满足f′(x)>f(x),则当a>0时,f(a)和eaf(0)大小关系为( )
已知可导函数f(x)(x∈R)满足f′(x)>f(x),则当a>0时,f(a)和eaf(0)大小关系为( )
A. f(a)<eaf(0)
B. f(a)>eaf(0)
C. f(a)=eaf(0)
D. f(a)≤eaf(0) 蓝色的海79011年前1
蓝色的海79011年前1 -
 qwezzz 共回答了17个问题
qwezzz 共回答了17个问题 |采纳率94.1%解题思路:设函数f(x)=e2x,则导函数f′(x)=2•e2x,显然满足f'(x)>f(x),由f(a)=e2a,eaf(0)=ea,比较得出结论.由题意知,可设函数f(x)=e2x,
则导函数f′(x)=2•e2x,显然满足f'(x)>f(x),
f(a)=e2a,eaf(0)=ea,当a>0时,显然e2a>ea ,即f(a)>eaf(0),
故选 B.点评:
本题考点: 利用导数研究函数的单调性.
考点点评: 本题考查求复合函数的导数的方法,以及指数函数的单调性,利用构造法求解是我们选择题常用的方法.1年前查看全部
- 设奇函数f(x)=ax3+bx+c(a≠0)的图象在点x=-1处的切线与直线6x+y+3=0平行,其导函数f′(x)的图
设奇函数f(x)=ax3+bx+c(a≠0)的图象在点x=-1处的切线与直线6x+y+3=0平行,其导函数f′(x)的图象经过点(0,-12).
(1)求实数a,b,c的值;
(2)求函数f(x)的单调递增区间,并求函数f(x)在[-1,3]上的最大值和最小值. wenchangma1年前1
wenchangma1年前1 -
 饺子最好吃 共回答了16个问题
饺子最好吃 共回答了16个问题 |采纳率93.8%解题思路:(1)先根据奇函数求出c的值,再根据导函数f′(x)的图象经过点(0,-12),求出b的值,最后依据在x=1处的导数等于切线的斜率求出c的值即可;
(2)先求导数f′(x),在函数的定义域内解不等式f′(x)>0和f′(x)<0,求得区间即为单调区间,根据极值与最值的求解方法,将f(x)的各极值与其端点的函数值比较,其中最大的一个就是最大值,最小的一个就是最小值;
(3)令g(x)=f(x)-6x=2x3-18x<0,求出解集,使得(0,m)是g(x)<0的子集即可,从而求出m的取值范围.(1)∵f(x)为奇函数,
∴f(-x)=-f(x),
即-ax3-bx+c=-ax3-bx-c,
∴c=0,
∴f′(x)=3ax2+b,
∵函数f(x)=ax3+bx+c(a≠0)的图象在点x=-1处的切线与直线6x+y+3=0平行,
∴f′(-1)=3a+b=-6,
∵导函数f′(x)的图象经过点(0,-12),
∴b=-12,
∴a=2;
(2)∵f(x)=2x3-12x,
∴f′(x)=6x2-12=6(x+
2)(x-
2),列表如下:
x (-∞,-
2)-
2 (-
2,
2)
2 (
2,+∞)
f′(x)点评:
本题考点: 利用导数研究曲线上某点切线方程;利用导数研究函数的单调性.
考点点评: 本题考查函数的奇偶性、单调性、二次函数的最值、导数的应用等基础知识,以及推理能力和运算能力.属于中档题.1年前查看全部
- 已知可导函数f(x)(x属于R)满足f‘(x)大于fx,则当a大于0时,fa和e*af(0)大小关系
已知可导函数f(x)(x属于R)满足f‘(x)大于fx,则当a大于0时,fa和e*af(0)大小关系
已知可导函数f(x)(x属于R)满足f‘(x)大于fx 芝麻021年前1
芝麻021年前1 -
 gbxh888 共回答了14个问题
gbxh888 共回答了14个问题 |采纳率85.7%设g(x)= f(x)ex,
∵f'(x)>f(x),
∴g′(x)=(f′(x)-f(x))exe2x>0
∴函数g(x)为R上的增函数
∵a>0
∴g(a)>g(0)
即f(a)ea> f(0)e0
∴f(a)>eaf(0)
故答案为:f(a)>eaf(0).1年前查看全部
- 已知关于x的函数 ,其导函数f′(x).
已知关于x的函数  ,其导函数f′(x).
,其导函数f′(x).
(1)如果函数 ,试确定b、c的值;
,试确定b、c的值;
(2)设当x∈(0,1)时,函数y=f(x)﹣c(x+b)的图象上任一点P处的切线斜率为k,若k≤1,求实数b的取值范围. lnmaywing1年前1
lnmaywing1年前1 -
 paolo6610 共回答了14个问题
paolo6610 共回答了14个问题 |采纳率100%(1)f′(x)=﹣x 2 +2bx+c
∵函数f(x)在x=1处有极值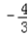
∴ 解得
解得  或
或 
(i)当b=1,c=﹣1时,f′(x)=﹣(x﹣1) 2 ≤0
所以f(x)在R上单调递减,不存在极值
(ii)当b=﹣1,c=3时,f′(x)=﹣(x+3)(x﹣1)
x∈(﹣3,1)时,f′(x)>0,f(x)单调递增
x∈(1,+∞)时,f′(x)<0,f(x)单调递减
所以f(x)在x=1处存在极大值,符合题意.
综上所述,满足条件的值为b=﹣1,c=3
(2)当x∈(0,1)时,函数y=f(x)﹣c(x+b)=﹣ x 3 +bx 2 ,
x 3 +bx 2 ,
设图象上任意一点P(x 0 ,y 0 ),则k=y′ =﹣
=﹣ +2bx 0 ,x 0 ∈(0,1),
+2bx 0 ,x 0 ∈(0,1),
因为k≤1,所以对任意x 0 ∈(0,1),﹣ +2bx 0 ≤1恒成立
+2bx 0 ≤1恒成立
所以对任意x 0 ∈(0,1),不等式b≤ 恒成立
恒成立
设g(x)=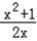 ,则g′(x)=
,则g′(x)= ,
,
当x∈(0,1)时,g′(x)<0
故g(x)在区间(0,1)上单调递减
所以对任意x 0 ∈(0,1),g(x 0 )>g(1)=1
所以b≤1.1年前查看全部
- x>0可导函数f(x)满足f(x)+2f(x/1)=3/x,求f(x)导函数
 逸生孤独1年前2
逸生孤独1年前2 -
 netmeteor 共回答了13个问题
netmeteor 共回答了13个问题 |采纳率100%解由f(x)+2f(x/1)=3/x.①
用1/x代替x代入①
得f(1/x)+2f(x)=3x.②
由①-②×2
f(x)-4f(x)=3/x-6x
即-3f(x)=3/x-6x
即f(x)=-1/x+2x
故f'(x)=1/x^2+21年前查看全部
- 给出定义:若函数f(x)在D上可导,即f′(x)存在,且导函数f′(x)在D上也可导,则称f(x)在D上存在二阶导函数,
给出定义:若函数f(x)在D上可导,即f′(x)存在,且导函数f′(x)在D上也可导,则称f(x)在D上存在二阶导函数,记f ″ (x)=(f′(x))′,若f ″ (x)<0在D上恒成立,则称f(x)在D上为凸函数.对于给出的四个函数:
①f(x)=sinx+cosx,②f(x)=lnx-2x,③f(x)=-x 4 +x 3 -x 2 +1,④f(x)=-xe -x
以上四个函数在 (0,
) 上是凸函数的是______(请把所有正确的序号均填上)π 2  会飞刀的小李1年前1
会飞刀的小李1年前1 -
 Arcadiav 共回答了15个问题
Arcadiav 共回答了15个问题 |采纳率93.3%对于①,f″(x)=-(sinx+cosx),x∈(0,
π
2 )时,f″(x)<0恒成立;
对于②,f″(x)=-
1
x 2 ,在x∈(0,
π
2 )时,f″(x)<0恒成立;
对于③,f″(x)=-2(6x 2 -3x+1),在x∈(0,
π
2 )时,f″(x)<0恒成立;
对于④,f″(x)=(2-x)•e -x 在x∈(0,
π
2 )时f″(x)>0恒成立,
所以f(x)=-xe -x 不是凸函数.
故答案为:①②③.1年前查看全部
- (2009•武昌区模拟)已知函数f(x)的导函数f′(x)=-3x2+6x+9.
(2009•武昌区模拟)已知函数f(x)的导函数f′(x)=-3x2+6x+9.
(1)求函数f(x)的单调区间;
(2)若f(x)在区间[-2,2]上的最大值为20,求它在该区间上的最小值. mixboy1年前1
mixboy1年前1 -
 san650033 共回答了13个问题
san650033 共回答了13个问题 |采纳率84.6%解题思路:(1)根据函数的单调性与导数的关系,令导数f′(x)>0(或<0),解不等式即可求出其单调递增区间和单调递减区间;
(2)根据函数的导数,设出函数f(x)=ax3+bx2+cx+d,求导,利用对应系数相等,求得a=-1,b=3,c=9,根据(1)可知函数在区间[-2,2]上的单调性,从而根据其最大值求出d的值,求出其最小值,(1)由f′(x)=-3x2+6x+9=-3(x+1)(x-3)<0,得x<-1或x>3,
由f′(x)=-3(x+1)(x-3)>0,得-1<x<3,
∴函数f(x)的单调减区间为(-∞,-1)和(3,+∞),单调增区间为(-1,3);
(2)设f(x)=ax3+bx2+cx+d,则f′(x)=3ax2+2bx+c,
∴3a=-3,2b=6,c=9,
即a=-1,b=3,c=9.
故f(x)=-x3+3x2+9x+d,
由(1)知f(x)在(-2,-1)上单调递减,在(-1,2)上单调递增,
又f(2)=22+d>f(-2)=2-d,
∴f(x)max=22+d=20,
∴d=-2,
∴f(x)=-x3+3x2+9x-2,
∴f(x)在区间[-2,2]上的最小值为f(-1)=-7.点评:
本题考点: 利用导数求闭区间上函数的最值.
考点点评: 本题考查利用导数研究函数的单调性和闭区间上函数的最值问题,根据函数的导数求出函数的解析式是解题的关键,增加了题目的难度,考查运算能力和逆向思维能力,属中档题.1年前查看全部
大家在问
- 1交联淀粉 玉米交联淀粉的合成工艺
- 2谁能赏析一下这三个句子?热烈欢迎语文达人回答.
- 3____ seen,it can never be forgotten.
- 4长方体的棱长之和24厘米,长方体的长宽高的数字完全不相同,而且都是整数厘米,长方体的体积是多少立方厘
- 5设o为坐标原点,抛物线y2=4x 与过焦点的直线交于A,B 两点,则0A*0B=
- 6环数in ENGLISH在英语中说某人打了***环应该怎么说?
- 7直接写出得数 2×34= 40÷2= 56+29= 84÷4= 6×40= 78-24= 96÷3= 82÷2= 46÷
- 8四年级英语划线提问对He is five中five的提问怎么写 对The pencil is two guan中two
- 9even可以放在句首吗,修饰一句话吗?even we can ask them by ourselves.
- 10若x/2=y/3=z/4,则3x-2y+5z/x+y+z=
- 11经历是美丽的 作文
- 12声东击( )( )如泰山(括号内添一个城市名)
- 13求解Carol_____(study) for the math test and_____(practice)____
- 14把下列成语找一个意思相近的成语低三下四 无中生有 改过自新 不闻不问 历历在目 目光如豆 目不暇接 画饼充饥
- 15有()有()填反义词?



