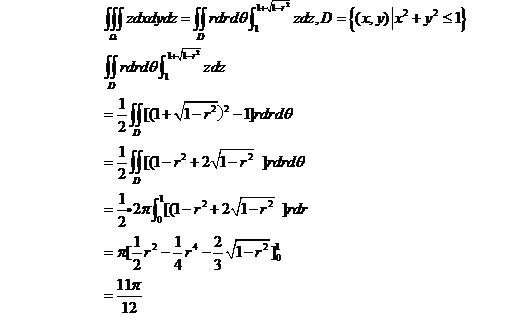∫∫∫zdxdydz,其中d由不等式z=6-x^2-y^2及z^2=x^2+y^2所围成的闭区域;
 紫虚山人2022-10-04 11:39:542条回答
紫虚山人2022-10-04 11:39:542条回答
已提交,审核后显示!提交回复
共2条回复
 mj4r 共回答了19个问题
mj4r 共回答了19个问题 |采纳率94.7%- z=6-x²-y²与z²=x²+y²的交线为:z=2或z=-3(舍)在xoy面的投影区域为:x²+y²≤4用柱坐标,z²=x²+y²可写为:z=√(x²+y²)=r,z=6-x²-y²可写为:z...
- 1年前
 chenbaihua 共回答了22个问题
chenbaihua 共回答了22个问题 |采纳率86.4%- 三重积分,好吧……没学
- 1年前
相关推荐
- ∫∫∫xzdxdydz,其中ω是曲面z=0,z=y,y=1,以及抛物柱面y=x^2所围成的闭区域
∫∫∫xzdxdydz,其中ω是曲面z=0,z=y,y=1,以及抛物柱面y=x^2所围成的闭区域
求详解 ddida1年前1
ddida1年前1 -
 若望的花雨 共回答了19个问题
若望的花雨 共回答了19个问题 |采纳率84.2%原式=∫xdx∫dy∫zdz
=(1/2)∫xdx∫y²dy
=(1/6)∫x(1-x^6)dx
=(1/6)∫(x-x^7)dx
=(1/6)*0
=01年前查看全部
- 计算三重积分∫∫∫zdxdydz,Ω由x^2+y^2+z^2=1与z=根号(x^2+y^2)所围的闭区域
计算三重积分∫∫∫zdxdydz,Ω由x^2+y^2+z^2=1与z=根号(x^2+y^2)所围的闭区域
最好柱坐标变换 无名独木桥1年前1
无名独木桥1年前1 -
 sodoit35 共回答了21个问题
sodoit35 共回答了21个问题 |采纳率85.7%∫∫∫zdxdydz=∫dθ∫rdr∫zdz (作柱面坐标变换)
=2π∫(1/2)[(1-r^2)-r^2]rdr
=π∫(r-2r^3)dr
=π(1/8)
=π/8.1年前查看全部
- 计算∫∫∫zdxdydz,其中Ω是由锥面z=h*√(x2+y2)/R与平面z=h(R>0,h>0)所围成的闭区域
计算∫∫∫zdxdydz,其中Ω是由锥面z=h*√(x2+y2)/R与平面z=h(R>0,h>0)所围成的闭区域
我看不太懂别人的解题过程,既然有了锥面但是没有看到引入sin和cos,也就是柱坐标进入解题过程, blueXken1年前1
blueXken1年前1 -
 gxgjb 共回答了21个问题
gxgjb 共回答了21个问题 |采纳率95.2%1年前查看全部
- Ω是由z=√[4-3(x^2+y^2)]及z=x^2+y^2围成的闭区域,求∫∫∫Ω zdxdydz
 随心的风1年前1
随心的风1年前1 -
 不想长大的qq 共回答了23个问题
不想长大的qq 共回答了23个问题 |采纳率91.3%z=√[4-3(x²+y²)]开口向下,z=x²+y²开口向上,因此它们所围区域的底部曲面为z=x²+y²,顶部曲面为z=√[4-3(x²+y²)],下面计算两曲面交线在xOy面的投影,
x²+y²=√[4-3(x²+y²)],得(x²+y²)²=4-3(x²+y²),即(x²+y²+4)(x²+y²-1)=0,得:x²+y²=1
因此投影为:x²+y²≤1,记为区域Dxy,则
∫∫∫zdxdydz 先积z
=∫∫ ∫[x^2+y^2-->√(4-3(x²+y²)) ] zdz dxdy 其中二重积分的积分区域为:Dxy
=1/2∫∫ z² |[x^2+y^2-->√(4-3(x²+y²)) ] dxdy
=1/2∫∫ (4-3(x²+y²)-(x²+y²)²) dxdy
用极坐标
=1/2∫∫ (4-3r²-r⁴)r drdθ 积分区域Dxy:x²+y²≤1
=1/2∫[0-->2π]dθ ∫[0-->1] (4r-3r³-r⁵) dr
=π[2r²-3/4r⁴-1/6r⁶] [0-->1]
=13π/121年前查看全部
- 求三重积分∫∫∫zdxdydz,其中积分区域为z=x^2+y^2,z=1,z=2所围区域
 xvczlkjlk23jlkfj1年前0
xvczlkjlk23jlkfj1年前0 -
 共回答了个问题
共回答了个问题 |采纳率
- 计算∫∫∫zdxdydz,其中Ω是由锥面z=h*(根号下x2+y2)/R与平面z=h(R>0,h>0)所围成的闭区域
计算∫∫∫zdxdydz,其中Ω是由锥面z=h*(根号下x2+y2)/R与平面z=h(R>0,h>0)所围成的闭区域
∫0 2πdθ ∫0 Rρdρ ∫hρ/R h zdz
为什么不对呀 delladeng1年前1
delladeng1年前1 -
 99flyant 共回答了20个问题
99flyant 共回答了20个问题 |采纳率95%你应该把正确答案放上来让别人参考.我觉得是对的呀1年前查看全部
- 计算三重积分∫∫∫zdxdydz,Ω是由曲面z=1+√(1-x^2-y^2)与z=1所围的闭区域.
计算三重积分∫∫∫zdxdydz,Ω是由曲面z=1+√(1-x^2-y^2)与z=1所围的闭区域.
rt
答案是11pi/12 牧野之风1年前2
牧野之风1年前2 -
 dinahdeng 共回答了18个问题
dinahdeng 共回答了18个问题 |采纳率94.4%1年前查看全部
- 计算三重积分I=∫∫∫(D)zdxdydz,其中D是上半球体x^2+y^2+z^2=o
 醇忆1年前2
醇忆1年前2 -
 mayerzh 共回答了15个问题
mayerzh 共回答了15个问题 |采纳率93.3%截面法
做截面Dz:x²+y²≤1-z²
∫∫∫(D) zdxdydz
=∫[0→1] zdz ∫∫ dxdy 其中二重积分的积分区域是Dz,Dz面积为:π(1-z²)
=π∫[0→1] z(1-z²)dz
=π∫[0→1] (z-z³)dz
=π[(1/2)z²-(1/4)z^4] |[0→1]
=π/41年前查看全部
- 计算三重积分∫∫∫zdxdydz,其中Ω由z=根号下x^2+y^2与z=4围成的闭区域.
 zhdo12291年前1
zhdo12291年前1 -
 lcbtg 共回答了22个问题
lcbtg 共回答了22个问题 |采纳率95.5%原式=∫(0,4)dz∫∫(Dz)zdxdy
=∫(0,4)zdz∫∫(Dz)dxdy
=∫(0,4)z×πz^2dz
=π∫(0,4)z^3dz
=π×1/4×z^4|(0,4)
=64π
其中Dz:x^2+y^2≤z^21年前查看全部
- 计算三重积分∫∫∫zdxdydz,其中Ω由z=x^2+y^2,z=0,x^2+y^2=1所围成的区域
计算三重积分∫∫∫zdxdydz,其中Ω由z=x^2+y^2,z=0,x^2+y^2=1所围成的区域
关键问题是xyz的范围怎么确定 Reginahj1年前1
Reginahj1年前1 -
 cxm518447 共回答了19个问题
cxm518447 共回答了19个问题 |采纳率94.7%采用柱坐标比较方便:
积分限:0≤θ≤2π,0≤r≤1,0≤z≤r²,dxdydz=rdrdθdz. 下面式子积分限没打,因为不好输入.
∫ dθ∫rdr∫zdz
=∫ dθ∫(1/2)r^5dr∫
=(1/12)∫dθ
=π/61年前查看全部
- 计算三重积分∫∫∫zdxdydz,其中Ω由z=x^2+y^2与z=4围成的闭区域.
计算三重积分∫∫∫zdxdydz,其中Ω由z=x^2+y^2与z=4围成的闭区域.
2π)dθ∫(0~2)ρdρ∫(ρ^2~4)zdz
为什么对z的积分的下限是ρ^2啊? jiachanglu1年前3
jiachanglu1年前3 -
 jhsj 共回答了12个问题
jhsj 共回答了12个问题 |采纳率91.7%因为,曲面z=x^2+y^2在柱坐标下的方程为z=ρ^2
这题如果是计算积分值的话,正解如下:
因为z=常数的平面与Ω截得区域的面积为πz
所以∫∫∫zdxdydz=∫(0~4)z(πz)dz=(1/3)π(z^3)︱(0~4)=64π/31年前查看全部
- 计算三重积分∫∫∫zdxdydz,其中Ω由z=x^2+y^2,z=0,x^2+y^2=1所围成的区域
计算三重积分∫∫∫zdxdydz,其中Ω由z=x^2+y^2,z=0,x^2+y^2=1所围成的区域
关键问题是xyz的范围怎么确定 我是新kk1号1年前1
我是新kk1号1年前1 -
 穿迷彩的xx 共回答了27个问题
穿迷彩的xx 共回答了27个问题 |采纳率81.5%采用柱坐标比较方便:
积分限:0≤θ≤2π,0≤r≤1,0≤z≤r²,dxdydz=rdrdθdz. 下面式子积分限没打,因为不好输入.
∫ dθ∫rdr∫zdz
=∫ dθ∫(1/2)r^5dr∫
=(1/12)∫dθ
=π/61年前查看全部
- 计算三重积分fffzdxdydz,区域由旋转抛物面2z=x^2+y^2和平面z=1围成
 eerdps1年前1
eerdps1年前1 -
 回锅肉好吃 共回答了13个问题
回锅肉好吃 共回答了13个问题 |采纳率100%∫∫∫Ω z dV
= ∫(0→1) z dz ∫∫ Dxy dxdy
= ∫(0→1) z • π(2z) dz
= 2π • (1/3)[ z³ ] |(0→1)
= 2π/3
或
∫∫∫Ω z dV
= ∫∫Dxy dxdy ∫(r²/2→1) z dz
= ∫(0→2π) dθ ∫(0→√2) r dr • (1/2)[ z² ] |(r²/2→1)
= π • ∫(0→√2) r • [ 1 - r⁴/4 ] dr
= (π/4)∫(0→√2) (4r - r⁵) dr
= (π/4) • [ 2r² - (1/6)r⁶ ] |(0→√2)
= (π/4) • [ 4 - (1/6)(8)]
= 2π/31年前查看全部
- 三重积分计算∫∫∫x+y+zdxdydz 为什么等于0?积分区域是x^2+y^2+z^2≦1.为什么书上都没算直接就给出
三重积分计算
∫∫∫x+y+zdxdydz 为什么等于0?积分区域是x^2+y^2+z^2≦1.为什么书上都没算直接就给出零?跟区域对称性和函数奇偶性有关吗?想了半天就是想不出来,向高手求救,想不出来急死了. judymak1年前1
judymak1年前1 -
 干女成什么 共回答了13个问题
干女成什么 共回答了13个问题 |采纳率76.9%这里有一个幻灯片
其实,三重积分,就是把一重积分和二重积分的扩展
三重积分及其计算
一,三重积分的概念
将二重积分定义中的积分区域推广到空间区域,被积函数推广到三元函数,就得到三重积分的定义
其中 dv 称为体积元,其它术语与二重积分相同
若极限存在,则称函数可积
若函数在闭区域上连续, 则一定可积
由定义可知
三重积分与二重积分有着完全相同的性质
三重积分的物理背景
以 f ( x, y, z ) 为体密度的空间物体的质量
下面我们就借助于三重积分的物理背景来讨论其计算方法.
二,在直角坐标系中的计算法
如果我们用三族平面 x =常数,y =常数, z =常数对空间区域进行分割那末每个规则小区域都是长方体
其体积为
故在直角坐标系下的面积元为
三重积分可写成
和二重积分类似,三重积分可化成三次积分进行计算
具体可分为先单后重和先重后单
①先单后重
——也称为先一后二,切条法( 先z次y后x )
注意
用完全类似的方法可把三重积分化成其它次序下的三次积分.
化三次积分的步骤
⑴投影,得平面区域
⑵穿越法定限,穿入点—下限,穿出点—上限
对于二重积分,我们已经介绍过化为累次积分的方法
例1 将
化成三次积分
其中 为长方体,各边界面平行于坐标面
解
将 投影到xoy面得D,它是一个矩形
在D内任意固定一点(x ,y)作平行于 z 轴的直线
交边界曲面于两点,其竖坐标为 l 和 m (l < m)
o
x
y
z
m
l
a
b
c
d
D
.(x,y)
例2 计算
其中 是三个坐标面与平面 x + y + z =1 所围成的区域
D
x
y
z
o
解
画出区域D
解
除了上面介绍的先单后重法外,利用先重后单法或切片法也可将三重积分化成三次积分
先重后单,就是先求关于某两个变量的二重积分再求关于另一个变量的定积分
若 f(x,y,z) 在 上连续
介于两平行平面 z = c1 , z = c2 (c1 < c2 ) 之间
用任一平行且介于此两平面的平面去截 得区域
则
②先重后单
易见,若被积函数与 x , y 无关,或二重积分容易计算时,用截面法较为方便,
就是截面的面积,如截面为圆,椭圆,三角形,正方形等,面积较易计算
尤其当 f ( x , y , z ) 与 x , y 无关时1年前查看全部
- 设Ω由平面z=1及z=x^2+y^2围成,计算三重积分∫∫∫zdxdydz
 狼来撩1年前0
狼来撩1年前0 -
 共回答了个问题
共回答了个问题 |采纳率
- 用球面坐标能不能解:计算三重积分I=∫∫∫(D)zdxdydz,其中D是上半球体x^2+y^2+z^2=o?
 HUST_Ricky1年前1
HUST_Ricky1年前1 -
 timidbear 共回答了16个问题
timidbear 共回答了16个问题 |采纳率100%根据D的性质,能用的
I = ∫∫∫_(D) z dxdydz
= ∫(0→2π) dθ ∫(0→π/2) dφ ∫(0→1) (rcosφ)(r²sinφ) dr
= ∫(0→2π) dθ ∫(0→π/2) cosφsinφ dφ ∫(0→1) r³ dr
= (2π)(1/2)(1/4)
= π/41年前查看全部
- ∫∫∫zdxdydz,其中D由不等式x^2+y^2+(z-a)^2
 pardlan1年前1
pardlan1年前1 -
 大黄蜂擎天柱 共回答了15个问题
大黄蜂擎天柱 共回答了15个问题 |采纳率93.3%球坐标变换:x=rsintcosb,y=rsintsinb,z=rcost,Jacobian行列式为r^2sint.
第一个不等式为r^21年前查看全部
大家在问
- 1The light was on all day long.I didn't know who ____.A.has t
- 22道九年级反比例函数题1.已知正比例函数y=ax的图像与反比例函数y=(6-a)/x的图像有一个交点的横坐标是1,求它们
- 3同一大小但不同重量的物体.已同样的力量旋转 那个会旋转的较久?
- 4关于运动的合成与分解,下列说法中正确的是( )
- 5找一找,100以内有哪些数是三个不同质数的乘积
- 6所有的化学公式
- 7洗衣粉原价12元,活动期间买五赠一,李阿姨买了5袋,问每袋便宜多少
- 8怎么提高自己的表达能力?就是想写书,写小说这类,具体就是心里边有许多想法,可是不知道如何写出来,比如心里有一个故事的大概
- 9(2014•广西)如图,用甲、乙两种方式在相同时间内将同一物体匀速提升相同高度时,拉力做功的功率为P甲、P乙,机械效率分
- 10已知圆心O的弦AB平行CD.求证:AB的垂直平分线垂直并且平分CD.
- 11电影放映机的镜头相当于一个凸透镜,当放电影时,物距、像距、焦距应满足的关系是
- 12如图,已知∠AOB,以O为端点作射线OC,且OE平分∠AOC,OF平分∠BOC.
- 13用40个单词以上描述你知道的圣诞节.
- 14植物细胞的细胞液存在于什么之间
- 15宰子昼寝。子曰:“朽木不可雕也,粪土之墙不可污也,与予与何诛?”请说下这段话的译文